In an earlier post, I mentioned a on creativity killers. This post spurred me to examine my own teaching strategies in a different light. Instead of simply determining whether my students know their stuff or not, I wanted to know whether the students leaving my class are prepared to be successful in a mathematical sense. Can they use mathematics in a creative way?
In examining my own teaching strategies, I began to realize that I might be stifling the creativity of my students. Many of you may think of me as a project based learning type of guy who values the process of finding a solution to a problem. But I am also an online learning kind of guy who utilizes MyLabs by Pearson. This platform allows me to easily assess my students with a variety of question types. These questions emphasize a correct answer and not the process by which those answers are obtained. It is this “right answer” type of learningthat forced me to confront the creativity question. Do questions like these help my students solve mathematical problems creatively?
Questions with a “right answer” certainly do serve some purpose. They help students master the basic information in the course. Before students can become mathematically creative, they need to have a sound foundation. Multiple choice questions and fill in the blank question help students to practice mathematics, but they cannot be the sole purpose of the class. The path through the course needs to start with these questions and move onto opportunities to apply the basic information.
You might think that the projects I use allow students to apply mathematics in a creative way. However, students complete the projects through scaffolding assignments and their work is documented in a preset format. Although each student completes a slightly different question, the questions generally have a “right answer”. As Briggs says, I have created a “very strict, tightly structured curriculum in which students have zero input and few opportunities to choose their own learning paths.” To be a creative endeavor, the projects need to allow students to choose a unique path to the solution.
This poses a difficult problem. I want to take out some of this structure and allow students to take on more choices in their learning. But I also have to make sure that the students have learned what they are supposed to have learned. After all, all of the courses I teach are transfer courses that articulate to each university in the state. Opening up the class so that students can choose their path to mastering the course objectives might threaten the course’s articulation to the universities. I focus oncreativity in applying the basic concepts and not in learning the basic concepts. Since the course objectives address learning the basic concepts (and not necessarily applying them), i avoid any potential articulation issues.
This semester I am teaching MAT 142 College Mathematics. This is a change for me as I have not taught this course for about 10 years. My approach to opening up the curriculum to allow for more student choice is pretty simple…baby steps. Next semester I am going to work on utilizing some of the adaptive learning strategies in MyLabs. But this semester I wanted to allow my students to be more creative in the projects they complete.
In the first project my students completed in College Mathematics, my students worked in teams to compare two potential salaries. Some members of the team examined salaries where the salary increased by a fixed amount each year. Other members of the team examined salaries where salary increased by a fixed percent each year. As a team, they formulated an answer to the question “Which salary is better?”
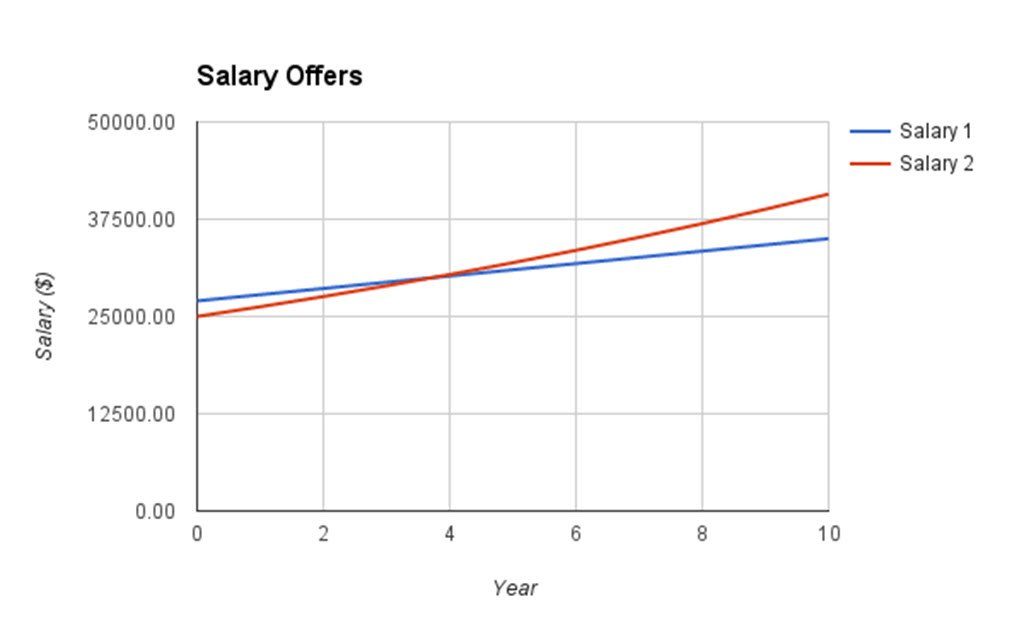
In the graph above, the salary with fixed dollar increases is in blue and the salary with fixed percent increases is in red. As you can see, the blue salary is higherinitially. But after about 4 years the red salary catches up. Most students focus on this point of intersection, but that point is the answer to a different question.
The question “When is the red salary higher than the blue salary?” has a straightforward answer. After about four years, the graphs cross and the red salary is higher. But when I ask which salary is better, the answer is “It depends.” What does the word “better” mean? By making the the question hazy, it opens the project up to several interpretations and paths that the teams might take to solve the problem.
As I mentioned before, most students answer the question initially by saying that you should take the blue salary if you plan to work for less than four years. If you will work for the company for more than four years, take the red salary. But that can’t be right…if the blue salary has been more for each of the first three years, you can’t expect that in working another year or two that the red salary will catch you up in accumulated salary. This key fact gets them to a different path where it is the amount of money accumulated from salary that is the key metric.
Problems that are phrased poorly allow students to probe different pathways before choosing one that is most appropriate. By giving them choices, they get a chance to try out several possible solutions. Students need to examine these solutions and determine if they are consistent with their interpretation of the problem.Brigg’s points out, “Limited intellectual freedom breeds limited intellectual engagement.”A question like this demandsengagement since there is not one “correct answer”.There are several ways to solve this problem depending on how they interpret “better”.
In next week’s post, I’ll describe how I assess student understanding of this problem. Like the problem itself, the assessment allows for a great deal of creativity since it involves making an infographic about the problem.












