
When it comes to statistical hypothesis testing, two common methods are often used: the Z-test and the T-test. These trials are used to determine whether a sample population is significantly different from a known population or not. However, choosing between these tests can be tricky. In this guide, we will explore the use and when to choose it over the T-test.
What is a Z-Test?

The Z-test is a statistical examination that is used to determine whether a sample population is significantly different from a known population. It is used when the population standard deviation is known. It is based on the standard normal distribution, which has a mean of 0 and a standard deviation of 1.
When to Use a Z-Test?
It is used when the population standard deviation is known. It is also used when the sample size is large (typically greater than 30) or when the distribution of the data is normal. It is commonly used in quality control, manufacturing, and finance.
How to Perform a Z-Test in Python?
Performing it is relatively straightforward. You can use the scipy.stats module to perform the examination. The following steps will guide you through the process:
Import the scipy.stats module

The scipy.stats module is a Python library that provides a wide range of functions for statistical analysis. It is a powerful tool for performing statistical trials and probability distributions. When performing these examinations, the scipy.stats module is essential. Here are the steps to import the scipy.stats module:
Step 1: Open a Python Environment
The first step is to open a Python environment, such as Jupyter Notebook or Spyder.
Step 2: Import the Scipy.Stats Module
To import the scipy.stats module, enter the following code:
python
Copy code
from scipy.stats import norm
This code imports the norm function from the scipy.stats module. The norm function is used to perform statistical trials based on the normal distribution.
Step 3: Check the Installation
To ensure that the scipy.stats module is installed correctly, you can check the version by running the following code:
python
Copy code
import scipy.stats print(scipy.stats.__version__)
This code will print the version of the scipy.stats module that is installed.
Define the sample mean
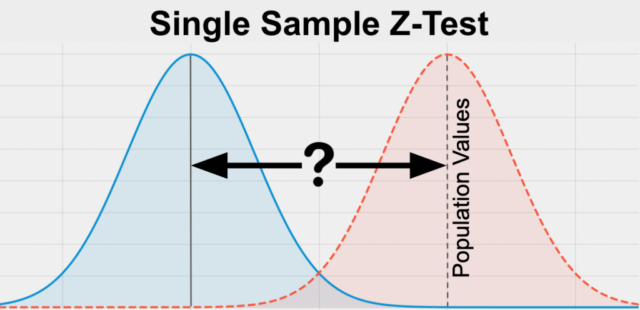
When performing statistical hypothesis variation, it is essential to understand the terms sample mean, the population means, sample standard deviation, and sample size. These terms are crucial in calculating the Z-score and p-value in a Z-test or T-test.
Sample Mean
The sample mean is the arithmetic average of a sample of data. It is calculated by adding up all the values in the sample and dividing the sum by the number of observations. The sample mean is used as an estimate of the population means.
Population Mean
The population means is the average value of a population. It is a fixed value and is usually unknown. In statistical hypothesis variation, we use the sample mean as an estimate of the population means.
Sample Standard Deviation
The sample standard deviation is a measure of the variability or spread of the sample data. It is calculated by finding the square root of the sample variance. The sample standard deviation is used to calculate the Z-score, which measures the number of standard deviations that the sample mean deviates from the population mean.
Sample Size
The sample size is the number of observations in the sample. It is essential in calculating the standard error, which is a measure of the variability of the sample mean. The standard error is used to calculate the confidence interval and the p-value.
Calculate the Z-score

python
Copy code
z_score = (sample_mean – pop_mean) / (sample_std / (sample_size ** 0.5))
Calculate the p-value
python
Copy code
p_value = norm.sf(abs(z_score)) * 2
Interpret the results
Interpreting the results is crucial in determining whether the sample population is significantly different from the known population. The results obtained can be interpreted by analyzing the p-value and the confidence interval.
P-Value
The p-value is a probability value that measures the likelihood of obtaining the observed sample mean, given the null hypothesis. In a Z-test, the null hypothesis assumes that there is no significant difference between the sample population and the known population. If the p-value is less than the significance level (usually 0.05), then we can reject the null hypothesis and conclude that the sample population is significantly different from the known population. If the p-value is greater than the significance level, we fail to reject the null hypothesis and conclude that there is no significant difference between the sample population and the known population.
Confidence Interval
The confidence interval is a range of values that is likely to contain the true population mean. A 95% confidence interval means that we are 95% confident that the true population mean lies within the calculated range. If the confidence interval does not contain the known population means, we can reject the null hypothesis and conclude that the sample population is significantly different from the known population. If the confidence interval contains the known population means, we fail to reject the null hypothesis and conclude that there is no significant difference between the sample population and the known population.
Example Interpretation
Suppose we conducted a Z-test with a significance level of 0.05 and obtained a p-value of 0.01. This result means that there is a 1% chance of obtaining the observed sample mean, given that the null hypothesis is true. Since the p-value is less than the significance level, we can reject the null hypothesis and conclude that the sample population is significantly different from the known population. Additionally, if the 95% confidence interval does not contain the known population means, we can further support this conclusion.
When to Choose Z-Test Over T-Test?

While it is useful in many scenarios, there are cases where the T-test may be more appropriate. The T-test is used when the population standard deviation is unknown, and it is also used when the sample size is small (typically less than 30). If the sample size is small and the population standard deviation is unknown, then the T-test is more appropriate.
Conclusion
The Z-test is a useful statistical test that is used to determine whether a sample population is significantly different from a known population. It is commonly used in quality control, manufacturing, and finance. Performing it is relatively straightforward using the scipy.stats module. When choosing between the Z-test and T-test, it is essential to consider the population standard deviation and sample size to determine which examination is more appropriate.












